Python Random Module

Randomness, is not something that can be achieved by a computer on its own. Computers, generally, work on a pre-written algorithm and by no means (except one) those algorithms can be truly random.

If you know the algorithm, you will most definitely know the output. But, a computer can pretend to generate randomness using some algorithms. These ‘random’ numbers generated by algorithms are called pseudo-random numbers.

Python has a module named the random module that implements multiple pseudo-random generators in the form of Python functions.

So, how would you go about generating truly random numbers using a computer?

It’s a curious yet simple thought, you make the computer read a real-life dataset, for example, pigeons trying to eat grains. And then create an algorithm based on that dataset. Well, that is not the focus of this article.

Let’s start studying the main focus of this article, i.e., Python’s random module.

Note We are going to call pseudo-random numbers random, and random numbers truly-random in this article.

First, let’s introduce to random() function. Almost every other function in the Random module depends on this function.

random()

random() function returns a random floating number in the range of 0.0 – 1.0. Most of the functions in the random module depend on this function to generate random numbers in the form of integers or sequences.

You can use this function in the following way.

Example

Note The random number is getting used only once. If you have to generate different random numbers, then you will have to run the function over and over again. The for loop can make the process easy.

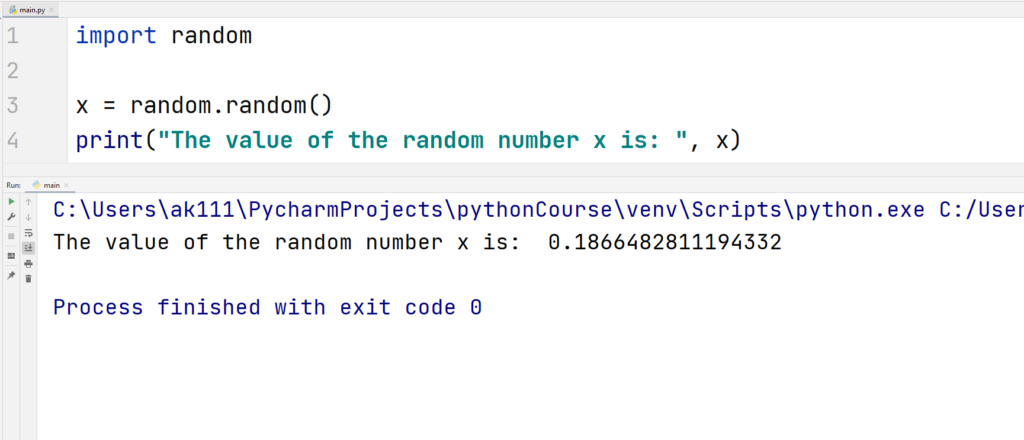
Example

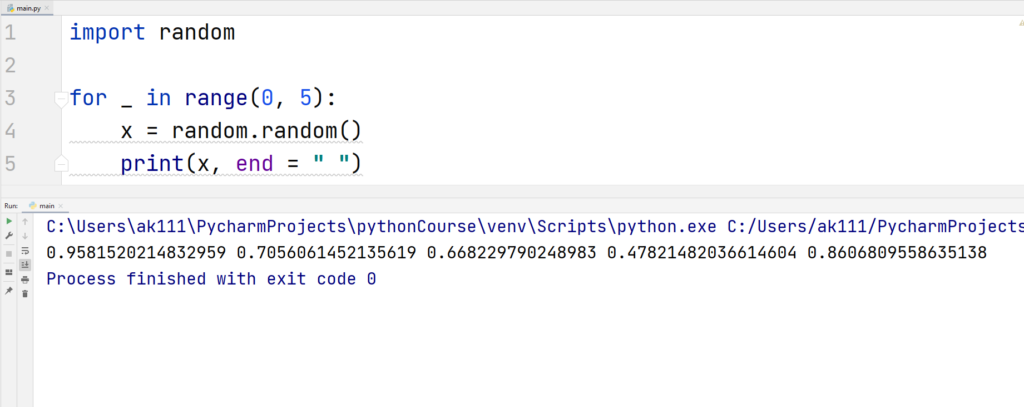
Let’s move on to the other functions from the Python random module.

seed()

The seed() function makes the random() function of the random module choose the same values at different executions.

For example, if you pass the value 5 into the seed() function, the random() function will generate a set of values that would be similar no matter how many times you execute your code.

Let’s understand it in a better way using an example.

Example

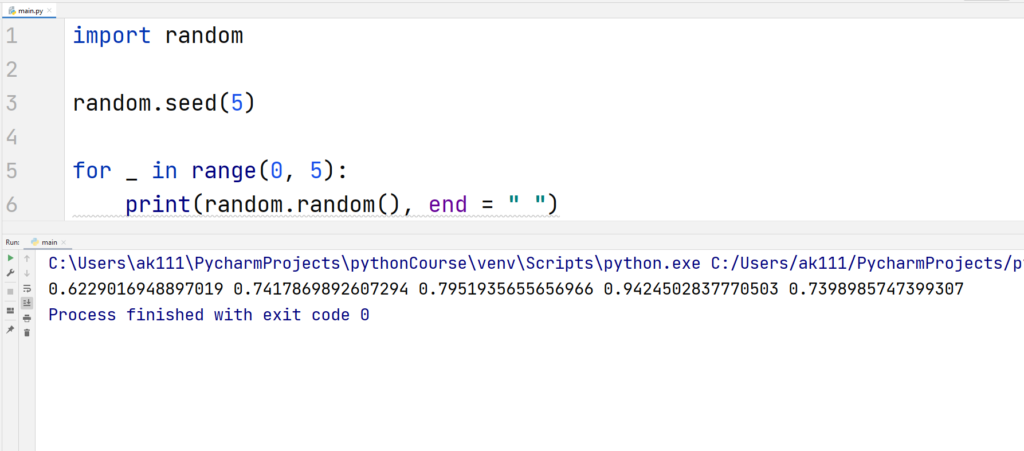
You will always get the same sequence if the value of seed is set equal to 5.

Important Note You should never use the random module in Python to encrypt data because it is not so random.

Generating Random Integers

1. randint(x, y)

The randint() function returns an integer between it’s two specified parameters. Let’s have an example to generate a random integer.

Example

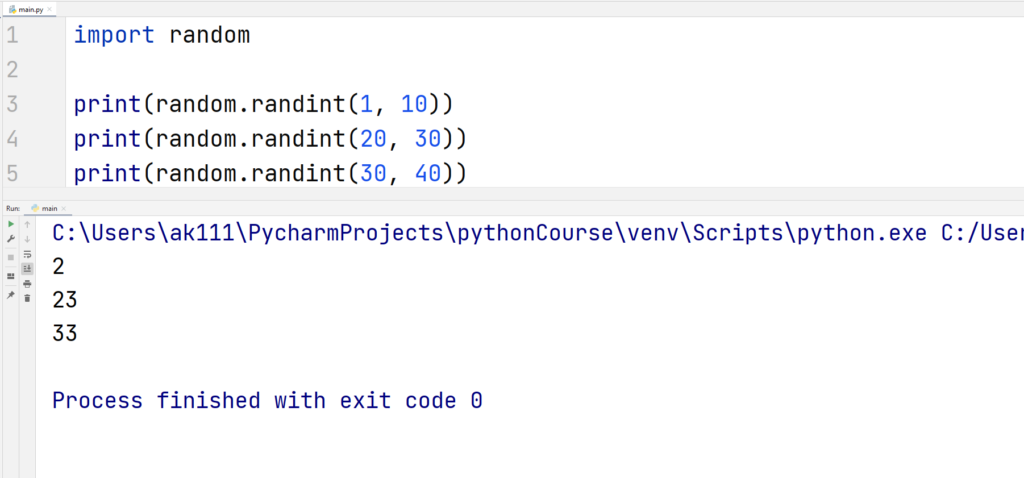
Another function named randrange(x, y, step_size) can also be used to get a random integer in the specified range.

2. randrange(x, y, step_size)

This method returns a random integer. By default the value of x starts at 0, and the step size is set equal to 1. This can be changed.

Let’s have an example of this function.

Example

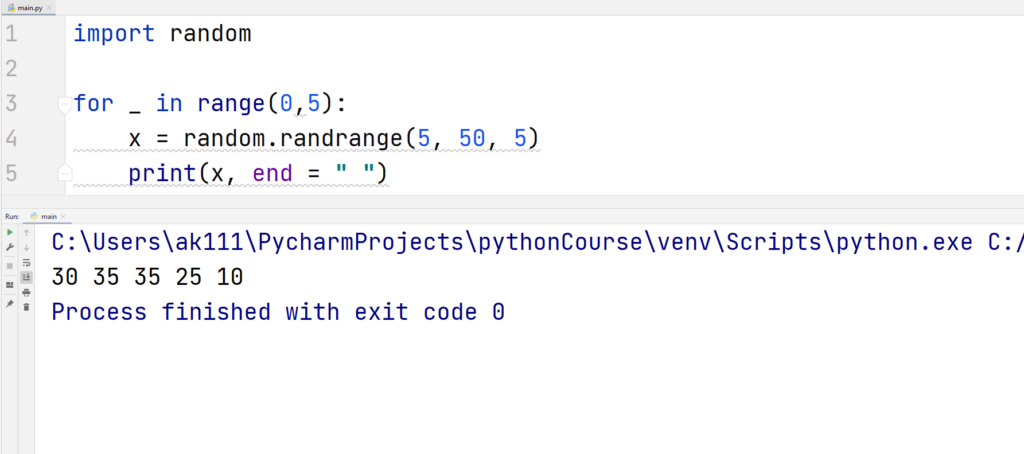
The above code will output random integers that are divisible by 5.

Random operations on set of elements

The following functions can be easily implemented with a 4–5 line of python script but it is good that they are already provided in the module.

1. choice()

Using the choice() function, you can randomly select an element from a set of elements. This function takes the index of the set instead of the elements itself.

Therefore, you can use this function on a string, a list of numbers, a list of strings, or any sequence.

Example

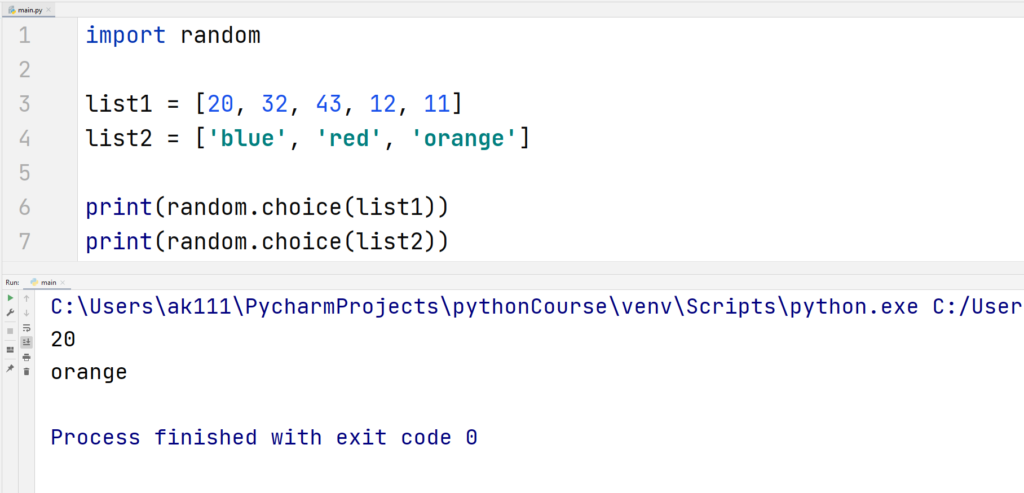
Bonus Tips

You can also randomly select a substring from a string.

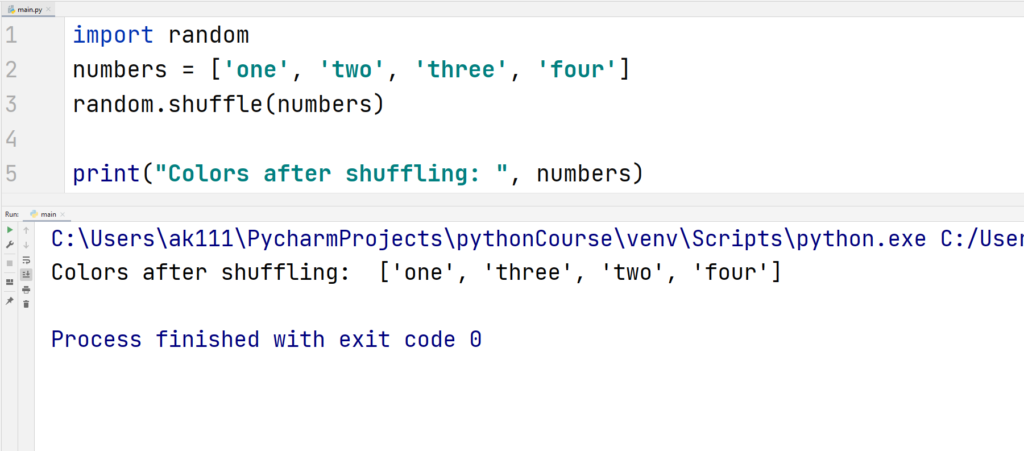
2. shuffle()

This function shuffles elements in a list in a random order.

Example

Note Unlike the functions discussed above, this function does not create a copy of the list. It makes changes in the list it is applied to.

Other functions in the random module

Function Name	Function Description
*sample(sequence, k)*	Returns a random list of specified k length from the sequence passed as the parameter.
*getrandbits(k)*	This function returns a non-negative integer representing k random bits.
*choices(sequence, k)*	Returns a random list of size k from the specified sequence.
*getstate()*	This function returns the state of the random number generator.
*setstate(state)*	This function reinstates the state of the random number generator.
*sample(sequence, k)*	Returns a k sized random sample from the specified sequence.
*uniform(a, b)*	This function returns a random floating number N lies between parameters a and b.
*gauss(mu, sigma)*	Gaussian distribution is used for the function to return a random floating number. mu is the mean and sigma is the variance.
*betavariate(alpha, beta)*	Returns a float value in the range of 0-1 based on the Beta distribution that is used in statistics. alpha is the scale parameter and beta is for shaping, i.e., the shaping parameter.
*expovariate(lambd)*	This function returns a float value based on the exponential distribution in statistics.
*gammavariate(alpha, beta)*	Note: This is not the gamma function. This function returns the float value based on the Gamma distribution.
*normalvariate(mu, sigma)*	This method returns a float value based on the normal distribution used in statistics. mu is the mean and sigma is the variance.
*lognormavariate(mu, sigma)*	This method returns a float value based on the log-normal distribution used in statistics. mu is the mean and sigma is the variance.
*paretovariate(alpha)*	The float value returned by this function depends on the Pareto distribution.
*weibullvariate(alpha, beta)*	Returns a float value that depends on the Weibull distribution.