Python Math Functions
Python provides math functions in the math module. The functions in math module are defined by the C standard.
This module has a ton of functions to perform various mathematical operations. But keep in mind that these functions cannot be used on complex numbers.
Commonly used Math Module Functions
math module has many functions to do the mathematical tasks. Let’s understand the most frequently used functions in detail.
At the end of the article all the other math functions are described in brief.
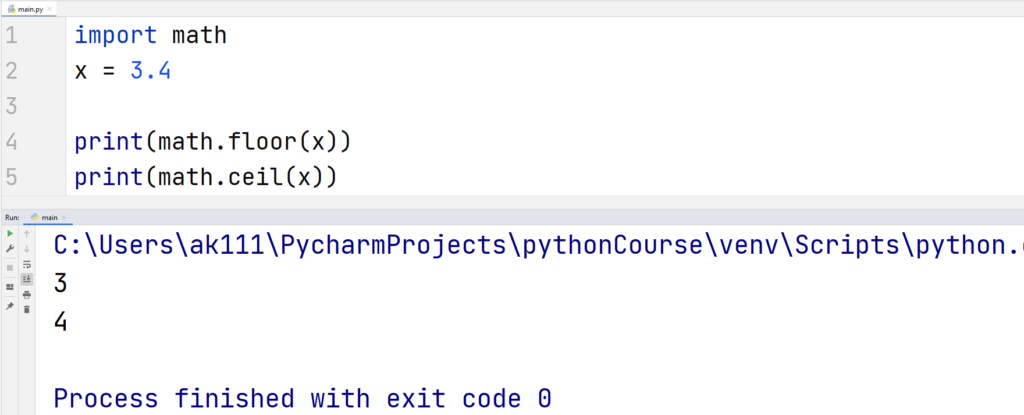
floor() and ceil()
The floor() function rounds off the float number to the nearest smallest integer. The ceil() function rounds off the float number to the nearest largest integer.
Example
Let’s have a look on all the important functions that the module provides.
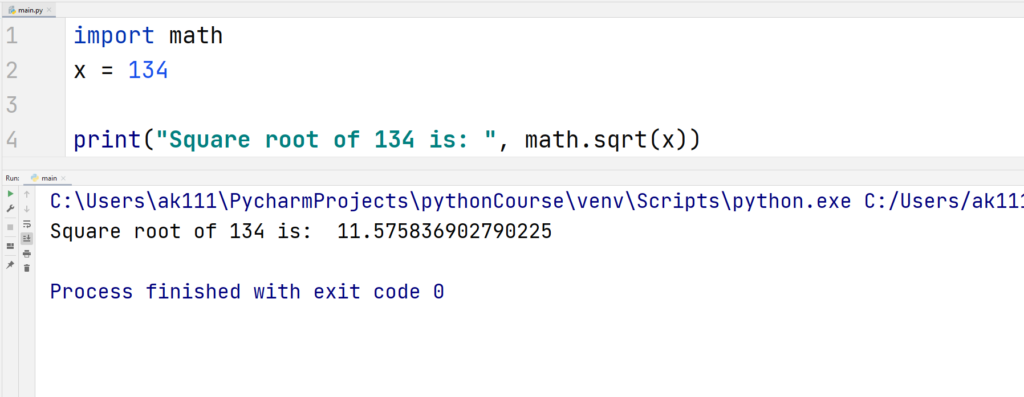
sqrt()
When you have to calculate the square root of a number, you are going to need sqrt() function.
Example
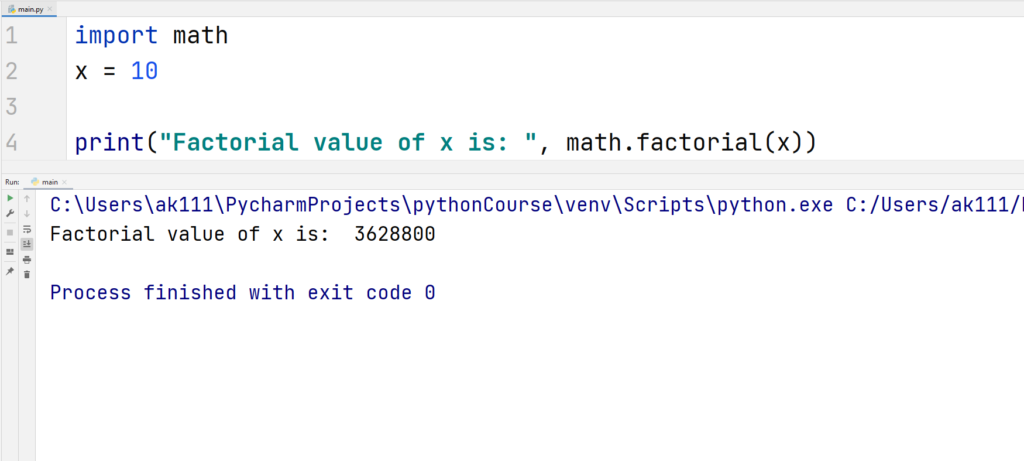
factorial()
factorial() function returns the factorial value of an integer as an integer.
Example
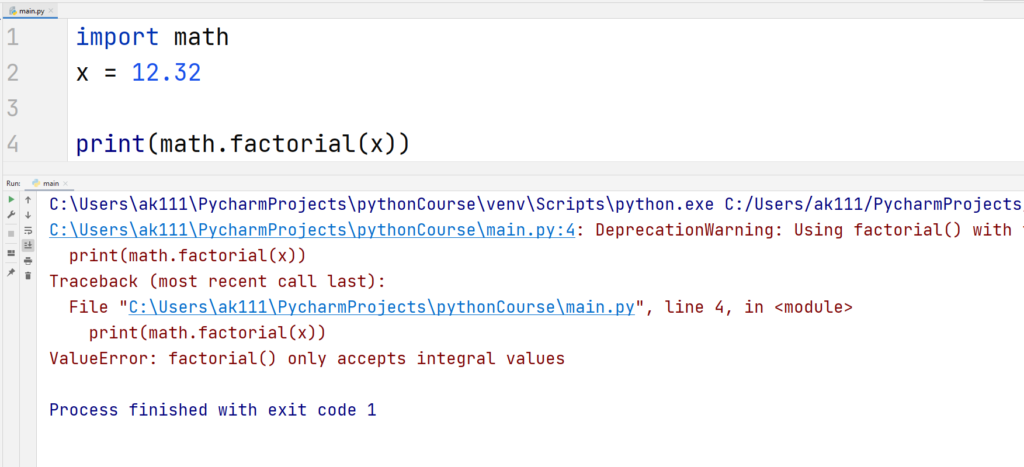
This function raises a ValueError if the value passed as parameter is not an integer or it is negative.
Example
copysign()
copysign() takes two parameters, x and y, and it returns a float value equal to x but with the sign of y.
Example
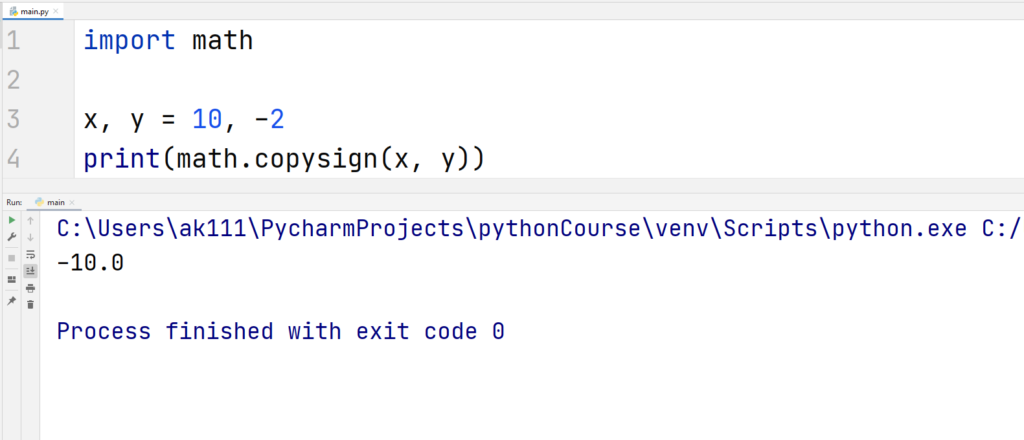
Also, the operating platforms that support signed zeros (- 0.0), the code math.copysign(2, -0.0) will return -2.
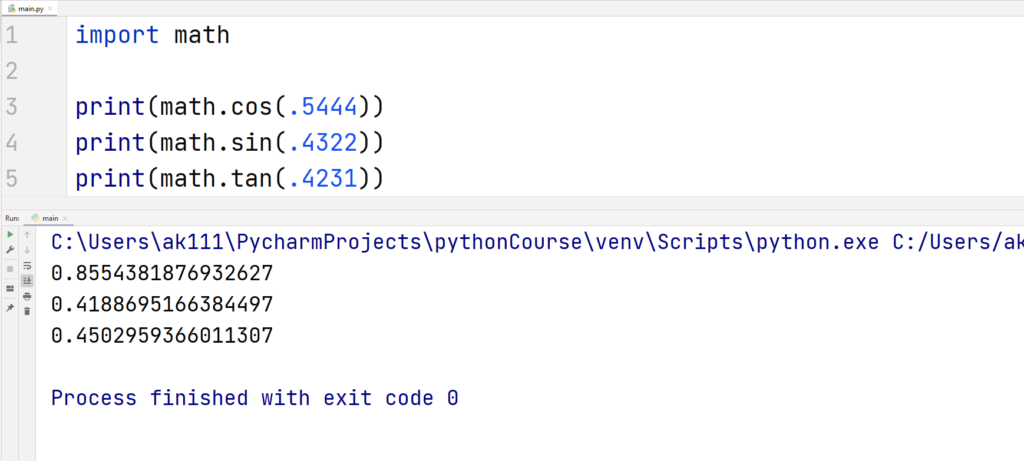
Trigonometric functions
You also have trigonometric functions like sin, cos, and tan in the math module. They can be used normally and they all return values in radians.
Example
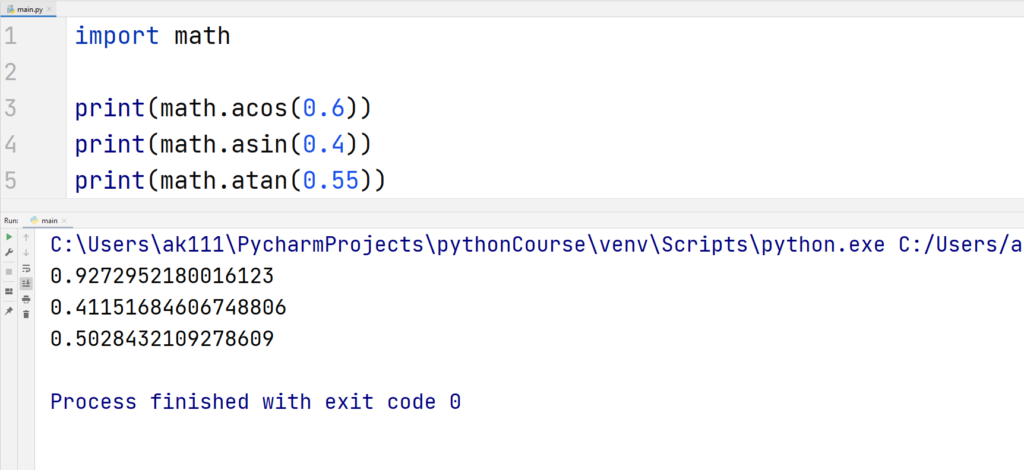
Other types of trigonometric functions like acos(x), asin(x), and atan(x) can also be accessed using this module.
Example
Greatest common divisor function
The gcd() function returns the greatest common divisor of it’s integer parameters. You can pass any number of integer parameters in this function.
Example

If some of the integers passed are negative then it will not affect the final result. The function would still consider the negative integers as positive and return a positive greatest common divisor.
Having all parameters as zeros will result in an output equal to zero.
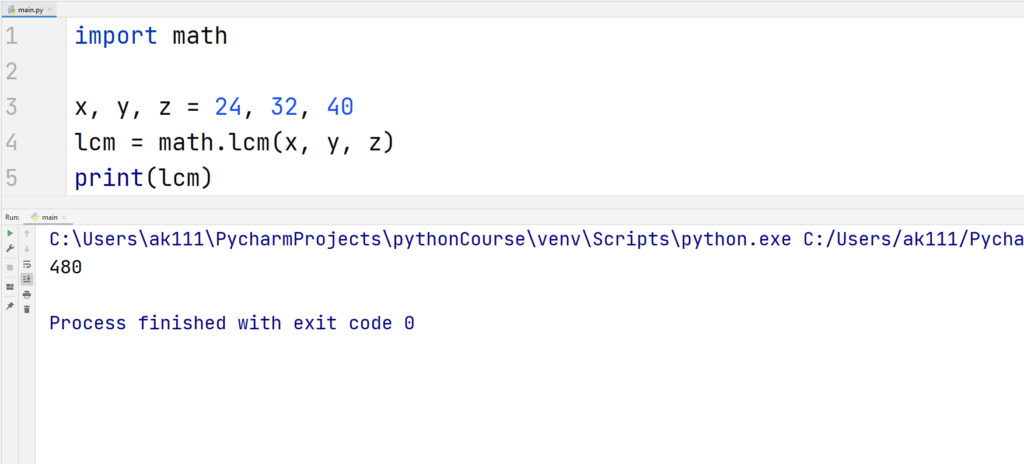
Least Common Multiple Function
The lcm() accepts multiple integers as arguments and then returns the least common multiple of the passed arguments.
Example
Exponential and Logarithmic Functions
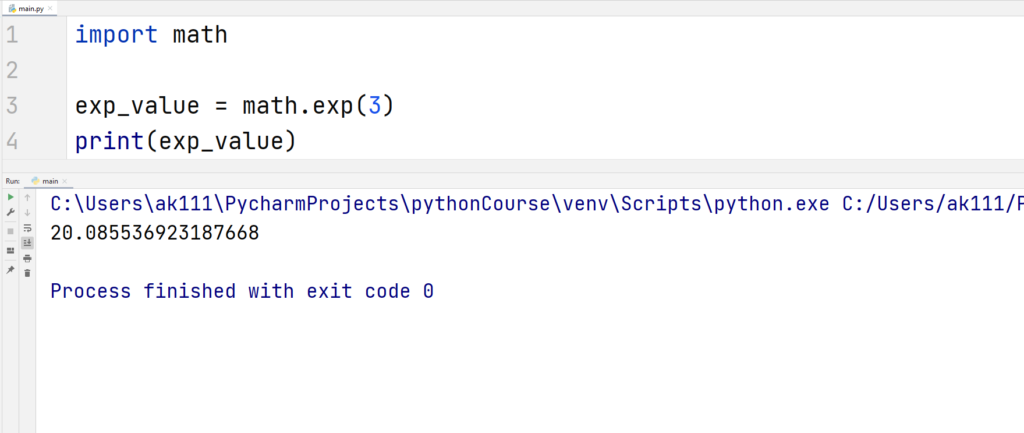
1. exp(x)
This function returns the value of e raised to the power of x. The exponential constant e is equal to 2.71828…., it is the base of natural logs.
Let’s check the below example.
Example
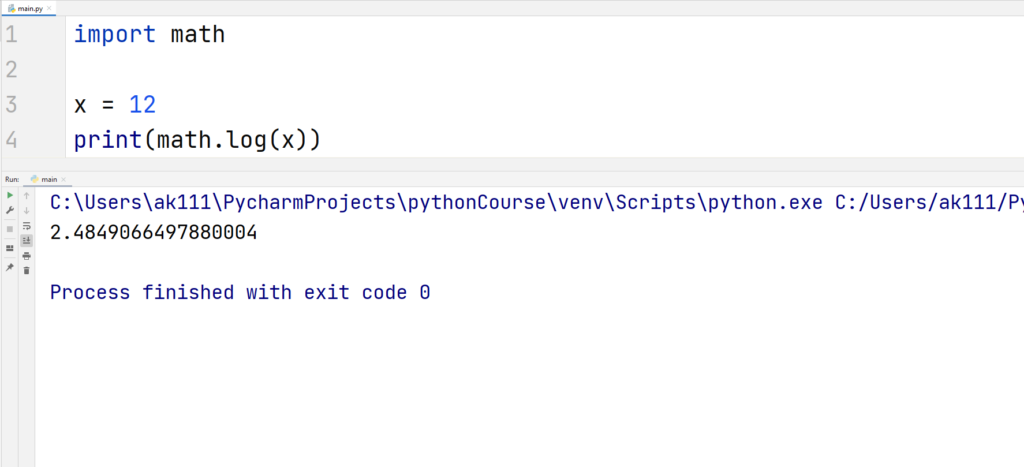
2. log(x[, base])
This function returns the logarithm of the passed integer to the base e if only one argument is passed.
Example
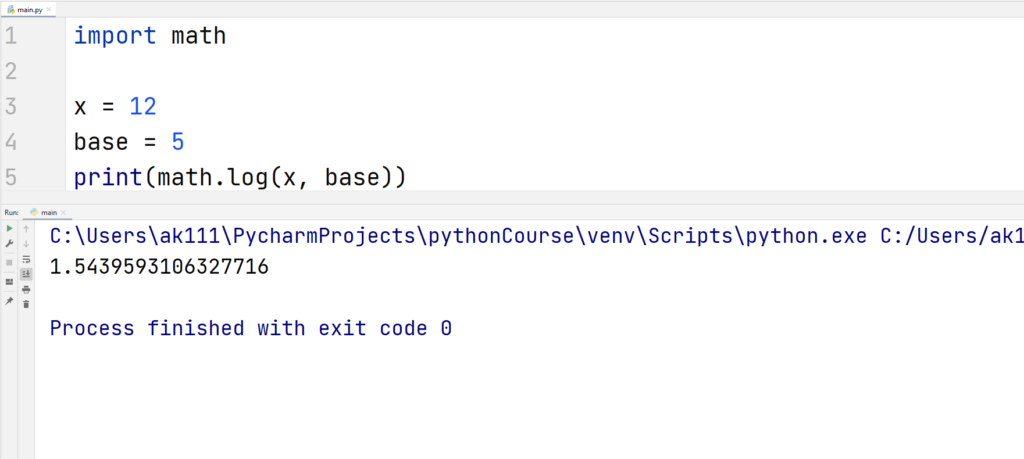
You can, however, pass a second argument to specify the base of the logarithmic value as below.
Example
Angular Conversion Functions
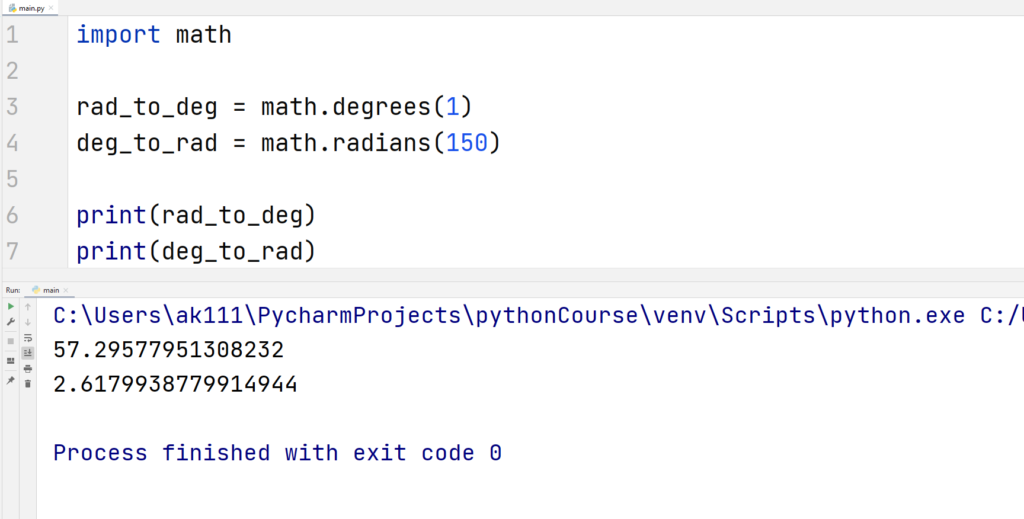
An angle x can be converted from radians to degrees or degrees to radians. This can be done using the functions degrees() and radians() respectively.
Consider this for an example.
Example
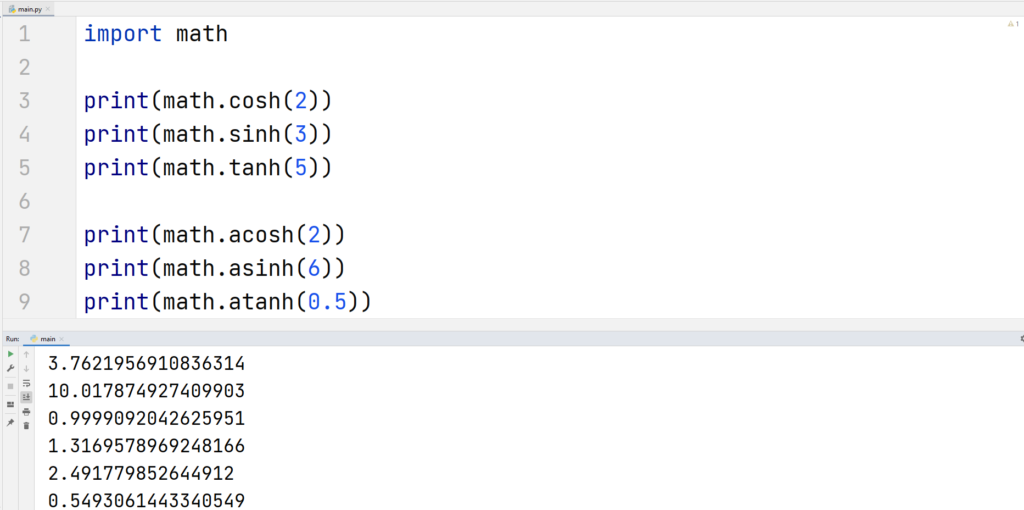
Hyperbolic Functions
Hyperbolic functions are trigonometric functions that relate to hyperbola instead of circles. They all can be accessed using the Python math module.
Example
Constants
The python math module contains some pretty common mathematical constants like pi , e, etc. They all can be accessed similarly using a dot separator. Let’s check in the below example.
Example
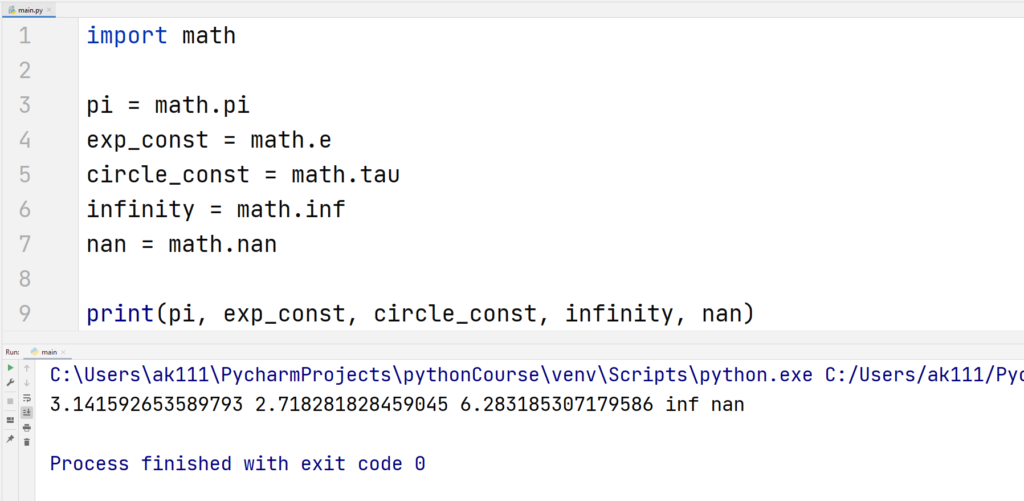
Here’s what they all mean:
- pi – This is one of the circle constants equal to 3.14159…., to the available precision.
- e – The exponential constant equal to 2.71828…, to the available precision.
- tau – This constant is equal to 2*pi. It’s equal to 6.283185…., to the available precision.
- inf – This constant is the positive infinity as a floating value. To get the negative floating infinity, you can use -math.inf.
- nan – This indicates that the value is not a number. You might have seen this in tables with numerical data.
List of all other math Module Functions
| Function Name | Function Description |
| comb(n, k) | The function returns the number of ways by which you can choose k items from n items without any repetition. (No order is implied) |
| fabs(x) | This function returns the absolute value of the parameter x. |
| fmod(x, y) | Returns the mod as a float value of two integers x and y. This function is more precise than a simple operation of x % y. |
| frexp(x) | Returns mantissa and exponent of x as a (mantissa, exponent) pair. |
| fsum(iter) | This function returns the sum of numbers in an iterable without losing precision, unlike the sum() function. To avoid loss of precision, this function tracks multiple intermediate partialities between the sums. |
| isclose(a, b, *, relative_tolerance, absolute_tolerance) | This function returns True if two specified values, a and b are close to each other. relative_tolerance: This is the maximum gap allowed between the two values. Relative to the larger of both values. For example, if you want to set a tolerance of 5%, make this parameter equal to 0.05. Default value is 1e-09. absolute_tolerance: This is the minimum gap allowed between the two values. This is very useful if you want to have comparisons near zero. The value of absolute_tolerance should be at least equal to zero. |
| isfinite(x) | Returns True if the passed value, x is a finite value. False if x is infinite. |
| isinf(x) | True if x is either a positive or negative infinity. False if x is finite. |
| isnan(x) | Returns True if x is NaN value (not a number). |
| issqrt(integer) | The value passed should be a positive integer. This function returns the square root of the value passed. |
| ldexp(x, i) | Returns the value x * (2**i). |
| modf(x) | This function returns the fraction and the integer part of x as (f, i) pair. Both values carry the sign of x and are floats. |
| nextafter(x, y) | This function returns the next floating-point value from x toward y. |
| perm(n, k=None) | The function returns the number of ways by which you can choose k items from n items without any repetition. (Order is implied). If k is not specified then the function returns the factorial of n. |
| prod(iterable, *, start = 1) | Returns the product of all elements in an iterable. start parameter decides the starting value for the product, it is by default set equal to 1. |
| remainder(x, y) | This function returns the IEEE 754-style remainder of x relative to y. If y is non-zero finite and x is finite, then the output of this function is equal to x – n*y. n is the integer closest to the exact value of x / y. |
| trunc(x) | This function returns the integer part of the value passed as the parameter. |
| ulp(x) | Unit in the last place (ulp) method returns the spacing between floating numbers. You can read about it here. |
| expm1(x) | Returns the exponential value of x after subtracting 1 from it. Similar results can be achieved using exp(x) – 1, but that would be less precise. |
| log1p(x) | Returns the log of 1+x with respect to base e. |
| log2(x) | Returns the value of the logarithm of x with base 2. Gives more accurate results than a log(x, 2). |
| log10(x) | Returns the value of the logarithm of x with base 10. Gives more accurate results than a log(x, 10). |
| pow(x, y) | Returns the value of x raised to the power y. This method converts both of its arguments to float type. |
| dist(p, q) | This function returns the Euclidean distance between two points p and q. Both are passed as iterable of coordinates. |
| hypot(*coordinates) | Returns the length of the vector from the origin to the described coordinates. |